[프로그래머스] - 두 원 사이의 정수 쌍 (Java & JavaScript)

두 원 사이의 정수 쌍

프로그래머스

코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.

programmers.co.kr

성능 요약

메모리: 75.7 MB, 시간: 10.58 ms

문제 설명

x축과 y축으로 이루어진 2차원 직교 좌표계에 중심이 원점인 서로 다른 크기의 원이 두 개 주어집니다. 반지름을 나타내는 두 정수 r1, r2가 매개변수로 주어질 때, 두 원 사이의 공간에 x좌표와 y좌표가 모두 정수인 점의 개수를 return하도록 solution 함수를 완성해주세요.
※ 각 원 위의 점도 포함하여 셉니다.

제한 사항

1 ≤ r1 < r2 ≤ 1,000,000

입출력 예

r1	r2	result
2	3	20

문제 풀이

먼저, 원 안에 점의 개수를 구하는 방법에 대해서 고민을 했습니다. 1 사분면에서 x축을 기준으로 점의 개수를 구하고, 4를 곱해 원 안에 전체 점의 개수를 구할 수 있습니다.

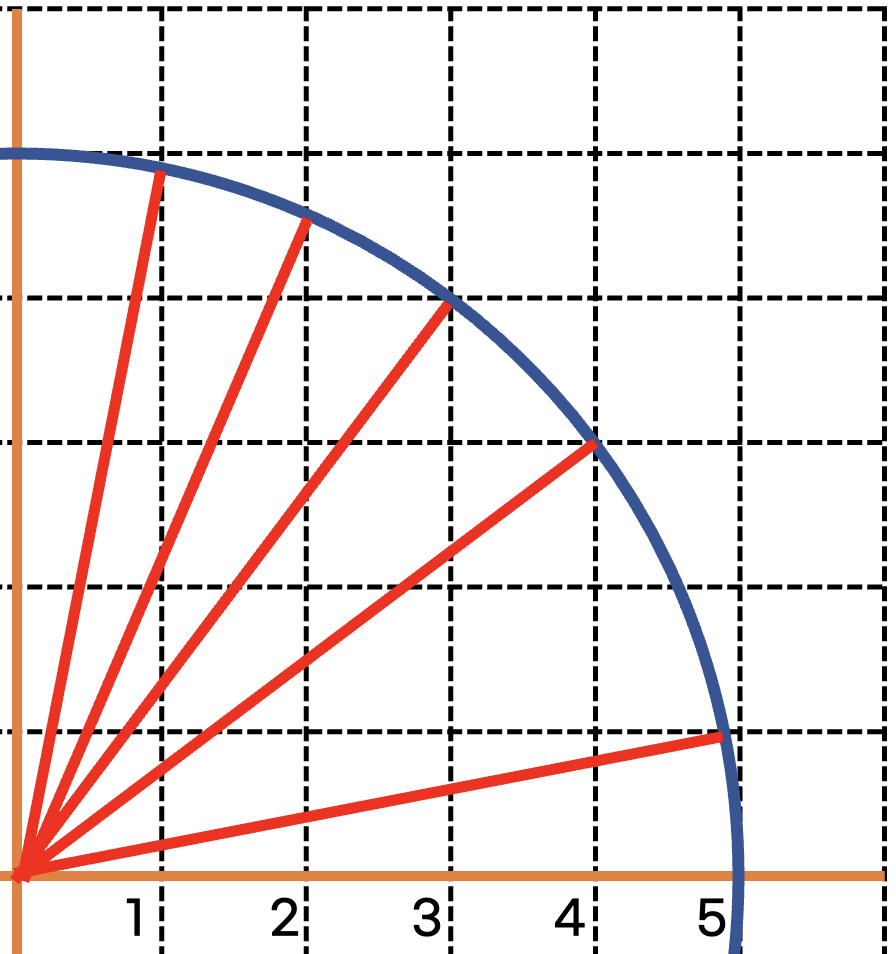
원의 정의 : 평면 위의 한 점에 이르는 거리가 일정한 평면 위의 점들의 집합은 반지름과 같다.

주황색 원에 속하는 부분은 원의 성질과 피타고라스 공식을 이용해서 구할 수 있습니다.

예를 들어 x 가 1 일 때 5^2 = 1^2 + y ^ 2 이 되므로 y는 4가 됩니다. 이 방식을 이용하면 x 축 별로 최대로 가질 수 있는 점의 개수를 알아낼 수 있습니다.

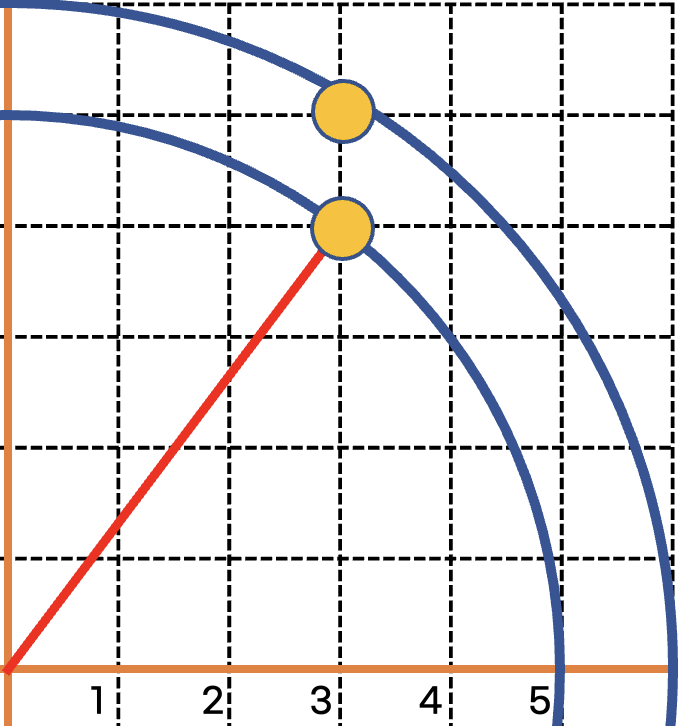
원 안에 점의 개수를 구하는 법을 알았으니, 이제 두 개의 원 안에서 점의 개수를 구하는 방법에 대해 고민을 해봐야 합니다.

주의할 점은 작은 원의 한 x축의 최대 y값이 정수인 경우입니다. 위의 그림에선 r=5이고 x축이 3일 때는 y가 4로 떨어지기 때문에 포함이 된다는 점입니다. 4.xx 인경우 포함이 안되지만 4.0인 경우는 포함해주어야 합니다.

이 점만 잘 풀이해 주면 1 사분면을 기준으로 x축을 순회하며, r2의 y 최댓값 - r1의 y최댓값을 계산하여 더해주고 마지막에 4를 곱하여 해결할 수 있습니다.

자바 풀이

import java.util.*;

class Solution {
    public long solution(long r1, long r2) {
        long answer = 0;

        for (int i = 1; i < r2; i++) {
            if (i < r1) {
                answer += getMaxY(i, r2, "r2") - getMaxY(i, r1, "r1");
            } else {
                answer += getMaxY(i, r2, "r2");
            }
        }
        answer *= 4;
        answer += (r2 - r1 + 1) * 4;
        return answer;
    }

    private int getMaxY(long x, long r, String rName) {
        double max = Math.sqrt(r * r - x * x);
        int maxToInt = (int) max;
        if (rName.equals("r1") && max - maxToInt == 0.0) {
            return maxToInt - 1;
        } else {
            return maxToInt;
        }
    }
}

x축별로 최대 y값을 가져오는 방법을 getMaxY라는 함수를 통해 가져와서 구현하였습니다. 이때 r1이면서, 최댓값이 정수인 경우 값을 포함해 주는 로직이 포함되어 있습니다.

자바스크립트 풀이

function solution(r1, r2) {
    let answer = 0;
    
    for (let i=1; i < r2; i++) {
         if (i < r1) {
            answer += getMaxY(i, r2, "r2") - getMaxY(i, r1, "r1");
        } else {
            answer += getMaxY(i, r2, "r2");
        }
    }
    answer *= 4;
    answer += (r2 - r1 + 1) * 4;
    return answer;
}

function getMaxY(x, r, rName) {
    const max = Math.sqrt(r * r - x * x);
    const maxToInt = parseInt(max);
    if (rName == "r1" && max - maxToInt == 0.0) {
        return maxToInt - 1;
    } else {
        return maxToInt;
    }
}

저작자표시